在凝聚态物理学中，人们对电子行为的理解正在经历一场深刻的变革。传统上只关注电子能量的能带理论已不再足够，现代观点开始将电子波函数中错综复杂的“量子几何”纳入考量。这种几何特性由量子几何张量编码，它由贝里曲率和量子度规构成，为我们描绘了一幅更完整的电子行为图景。

发表在《科学》的论文《The quantum metric of electrons with spin-momentum locking》特别深入探讨了量子几何中一个此前未被充分探索的关键部分，即在大量具有自旋-动量锁定特性的材料中存在一个非零的量子度规。这一发现意义深远，它不仅影响着基础物理学，也为下一代电子设备，特别是自旋电子学的发展，铺平了道路。

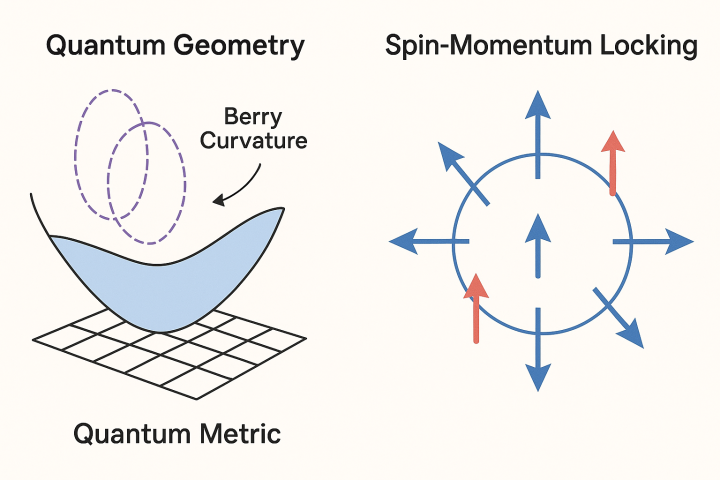
基础：量子几何与自旋-动量锁定

要理解这篇论文的重要性，我们必须首先掌握它的两个核心概念：量子几何和自旋-动量锁定。

1.量子几何：超越能带的维度

传统的能带理论描述了晶格中电子的能量，但它无法捕捉到电子量子态的微妙几何特性。量子几何通过引入量子几何张量来弥补这一不足。这个张量包含两个部分：

贝里曲率：张量的虚部，贝里曲率就像动量空间中的一个“磁场”。它在动量空间上的积分是量子化的，并产生了像陈数这样的拓扑不变量。贝里曲率是许多著名现象的根源，例如反常霍尔效应，即在没有外部磁场的情况下，电流会产生一个横向电压。

量子度规：张量的实部，量子度规衡量动量空间中两个无限接近的量子态之间的“距离”。它是这些量子态“可区分性”的度量。与贝里曲率（与相位有关）不同，量子度规与波函数重叠的幅度有关。一个较大的量子度规意味着波函数随动量变化得更快，这会对材料的物理性质产生切实的效应。

2.自旋-动量锁定：自旋与方向的共舞

自旋-动量锁定是一种相对论效应，源于自旋-轨道耦合，它将电子的内禀自旋与它的线性动量紧密相连。在强自旋-轨道耦合的材料中，电子的自旋方向与其运动方向严格关联。这是拓扑绝缘体和Rashba体系等材料的决定性特征。例如，在具有Rashba自旋-轨道耦合的二维电子气中，电子的自旋总是垂直于其动量，形成一个螺旋状的自旋结构。这种独特的耦合关系催生了许多现象，包括后向散射的抑制，以及通过电荷电流产生自旋电流的能力（即Rashba-Edelstein效应）。

论文的核心贡献

这篇论文的核心论点非常大胆：自旋-动量锁定本身就与一个非零的量子度规息息相关，即便在贝里曲率为零的系统中也是如此。这是一个至关重要的区别。长期以来，对量子几何的大部分研究都集中在贝里曲率上，因为它与稳健、量子化的拓扑效应有关。相比之下，量子度规的研究较少，其物理表现也一直难以捉摸，主要局限于一些非常特殊的材料，如拓扑反铁磁体。

研究人员通过分析像LaAlO₃/SrTiO₃界面处的二维电子气等材料来证明了这一论点。他们表明，该体系中具有自旋-动量锁定的电子能带，尽管贝里曲率为零，却拥有一个非平凡的量子度规。

为了证明这一点，他们设计了一个巧妙的实验。他们在材料上施加了一个平面内磁场，从而微妙地打破了时间反演对称性。这一扰动激发了一个此前未被观测到的现象：一种非线性的平面内磁阻。这种磁阻被称为量子度规磁阻，只能用存在非零量子度规来解释。这一结果具有开创性意义，因为它为在一种常见且被广泛研究的材料体系中，提供了量子度规的直接、可实验验证的物理特征。

影响与未来方向

这篇论文的发现对物理学和技术领域的多个方面都具有巨大意义。

1.扩展量子几何的范畴：通过在一个新的材料类别中展示与量子度规相关的可观测物理量，该论文拓宽了量子几何的研究范畴。它表明量子度规不仅仅是一个抽象的数学概念，它更是大量自旋-轨道耦合体系的一个基本属性。这为探索电子态丰富的几何图景开辟了新途径，甚至在那些不表现出由贝里曲率驱动的强拓扑效应的材料中也是如此。

2.迈向新一代自旋电子学：最直接和最具影响力的应用在于自旋电子学，该领域旨在利用电子的自旋（除了电荷之外）进行信息处理。这篇论文为操纵和探测电子的量子态提供了一个新工具。

新型设备：量子度规磁阻（QMMR）的发现为设计自旋电子器件提供了新的原理。通过电学方式控制量子度规，未来或许能够开发出基于全新物理原理的低功耗逻辑门和传感器。

增强控制：自旋-动量锁定是实现电荷电流到自旋电流转换以及反向转换的强大机制。量子度规为此过程增加了新的控制维度，使得对自旋态的操控更加精确和高效。

结论

新论文是一项具有里程碑意义的研究，它弥合了理论量子几何与实验凝聚态物理之间的鸿沟。它表明，神秘的量子度规并非一个利基概念，而是理解大量具有自旋-动量锁定材料中电子行为的关键要素。通过在一个常见材料中提供量子度规的切实可测的物理特征，这项研究不仅加深了我们对量子现象的基础理解，也为设计和工程化先进电子和自旋电子技术提供了新途径。这项工作有望成为未来研究的催化剂，推动量子材料世界的界限。